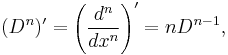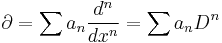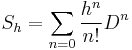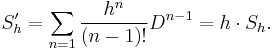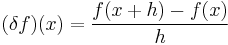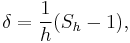Pincherle derivative

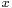In mathematics, the Pincherle derivative of a linear operator \scriptstyle{ T:\mathbb K[x] \longrightarrow \mathbb K[x] } on the vector space of polynomials in the variable \scriptstyle x over a field 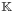\scriptstyle{ \mathbb K} is another linear operator \scriptstyle{ T':\mathbb K[x] \longrightarrow \mathbb K[x] } defined as

T' = [T,x] = Tx-xT = -\operatorname{ad}(x)T,\,

so that

T'\{p(x)\}=T\{xp(x)\}-xT\{p(x)\}\qquad\forall p(x)\in \mathbb{K}[x].

In other words, Pincherle derivation is the commutator of 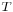\scriptstyle{T} with the multiplication by 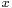\scriptstyle x in the algebra of endomorphisms \scriptstyle{ \operatorname{End} \left( \mathbb K[x] \right) }.

This concept is named after the Italian mathematician Salvatore Pincherle (1853–1936).

Properties

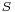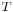The Pincherle derivative, like any commutator, is a derivation, meaning it satisfies the sum and products rules: given two linear operators \scriptstyle S and \scriptstyle T belonging to \scriptstyle \operatorname{End} \left( \mathbb K[x] \right)

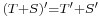  1. \scriptstyle{ (T %2B S)^\prime = T^\prime %2B S^\prime } ;
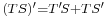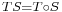  2. \scriptstyle{ (TS)^\prime = T^\prime\!S %2B TS^\prime } where \scriptstyle{ TS = T \circ S} is the composition of operators ;
  3. \scriptstyle{ [T,S]^\prime = [T^\prime , S] %2B [T, S^\prime ] } where \scriptstyle{ [T,S] = TS - ST} is the usual Lie bracket.

The usual derivative, D = d/dx, is an operator on polynomials. By straightforward computation, its Pincherle derivative is

D'= \left({d \over {dx}}\right)' = \operatorname{Id}_{\mathbb K [x]} = 1.

This formula generalizes to

(D^n)'= \left({{d^n} \over {dx^n}}\right)' = nD^{n-1},

by induction. It proves that the Pincherle derivative of a differential operator

\partial = \sum a_n {{d^n} \over {dx^n} } = \sum a_n D^n

is also a differential operator, so that the Pincherle derivative is a derivation of \scriptstyle \operatorname{Diff}(\mathbb K [x]) .

The shift operator

S_h(f)(x) = f(x%2Bh) \,

can be written as

S_h = \sum_{n=0} {{h^n} \over {n!} }D^n

by the Taylor formula. Its Pincherle derivative is then

S_h' = \sum_{n=1} {{h^n} \over {(n-1)!} }D^{n-1} = h \cdot S_h.

In other words, the shift operators are eigenvectors of the Pincherle derivative, whose spectrum is the whole space of scalars 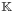\scriptstyle{ \mathbb K }.

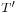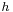If T is shift-equivariant, that is, if T commutes with Sh or \scriptstyle{ [T,S_h] = 0}, then we also have \scriptstyle{ [T',S_h] = 0}, so that \scriptstyle T' is also shift-equivariant and for the same shift \scriptstyle h.

The "discrete-time delta operator"

(\delta f)(x) = {{ f(x%2Bh) - f(x) } \over h }

is the operator

\delta = {1 \over h} (S_h - 1),

whose Pincherle derivative is the shift operator 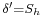\scriptstyle{ \delta ' = S_h }.

See also

External links